
Figura 1. Uma das ‘computadoras humanas’ do filme faz cálculos no quadro-negro CRÉDITO: DIVULGAÇÃO
O filme norte-americano Estrelas além do tempo (Hidden figures, no título original), de 2016, dirigido por Theodore Melfi, narra a impressionante história real das mulheres negras que trabalhavam como ‘computadores humanos’ na NASA (agência espacial dos EUA), durante a corrida espacial na década de 1960.
O termo é esse mesmo: ‘computadores humanos’. O trabalho dessas pessoas era ‘computar’, isto é, fazer contas – em geral, longas e trabalhosas, que, hoje, podem ser executadas por máquinas de mesmo nome.
O problema central na trama do filme era como colocar e retirar, da órbita da Terra, de forma segura, uma cápsula com tripulante humano. Os cálculos, complexos, para resolver esse problema demandavam extrema precisão: um mínimo erro na trajetória ou velocidade da cápsula poderia botar em risco a vida do astronauta.
O contexto histórico do filme – a Guerra Fria, tensão política e militar entre EUA e a então União Soviética (URSS) – acrescentava outro ingrediente à trama: era fundamental, para a NASA, que esse problema fosse resolvido rapidamente. A chamada corrida espacial, inserida na Guerra Fria, era uma disputa por demonstrações de poder tecnológico (e, portanto, bélico) entre as duas potências.
Essa disputa, em sua essência, era ver qual dos dois países poria um humano em órbita da Terra. Vale lembrar que a URSS já havia posto em órbita terrestre o primeiro satélite artificial, o Sputnik-1, lançado em 1957.
O filme é reconhecido pela denúncia de discriminações estruturais de etnia e gênero que atravessam (ainda hoje) relações de trabalho, ambientes institucionais e meios científicos – e que, com frequência, são silenciadas ou minimizadas.
Além desse mérito, Estrelas além do tempo mostra como, à época, era preciso fazer à mão e rapidamente contas longas, trabalhosas e precisas, sem a ajuda de computadores (figura 1). Outra leitura possível: uma apropriação tecnicista da ciência pode produzir relações precárias de trabalho, em ambientes profissionais tóxicos.
A determinação de órbitas é exemplo de problema para o qual é importante o cálculo diferencial e integral (ou, simplesmente, cálculo), subárea da matemática. Essa disciplina está presente na graduação das ciências exatas (por exemplo, matemática, física, química, engenharia) e na de outras áreas, como economia e ciências da saúde.
Mas o que é cálculo exatamente?
Dada a profundidade de seu conteúdo teórico e a diversidade de suas aplicações, essa pergunta pode ter respostas bem diferentes – algumas destacando seus principais conceitos; outras, seus procedimentos, métodos ou aplicações.
Por causa de sua capacidade em resolver ampla variedade de problemas, seu ensino é justificado em currículos de graduação de várias e distintas áreas.
Mas há uma mítica em torno do cálculo: disciplina difícil e responsável por altos níveis de reprovação e evasão – às vezes, chega a ser comparado a um ‘filtro’ pelo qual passariam apenas os ‘mais capazes’.
Comumente, estudantes atribuem essa dificuldade ao fato de o cálculo lidar com ideias aparentemente muito diferentes daquelas estudadas na matemática do Ensino Médio – quase como se a matemática passasse a ser outra coisa, estranha e desconhecida.
Os conceitos fundamentais hoje presentes nas ementas dessa disciplina se desenvolveram ao longo de séculos, a partir de problemas tanto das ciências naturais quanto da filosofia, da Antiguidade até tempos recentes.
De forma geral, esses conceitos têm a ver com noções de infinitos e infinitésimos – isto é, com comportamentos de variáveis assumindo valores numéricos arbitrariamente grandes, pequenos ou próximos de algum valor fixo.
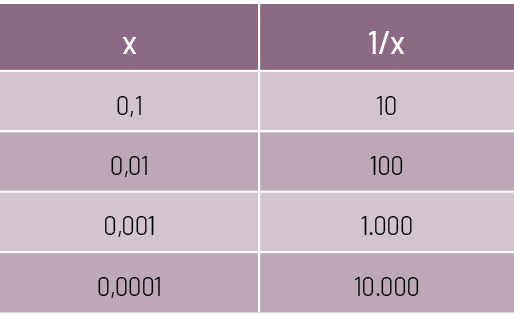
Esses comportamentos são expressos na matemática contemporânea pelos conceitos chamados de limites. Por exemplo, se tomamos uma variável (digamos, x) com valores positivos indefinidamente próximos de zero, os valores de 1/x ficarão arbitrariamente grandes.
De forma mais precisa, podemos fazer os valores de 1/x tão grande quanto queiramos, escolhendo, para isso, valores de x suficientemente próximos de zero (figura 2). Nesse caso, dizemos que 1/x tende a infinito quando x tende a zero.
Assim, os conceitos fundamentais do cálculo, em certo sentido, trazem noções de infinitos e infinitésimos para o campo dos objetos manipuláveis em matemática.
Essas ideias permitem desvendar sutilezas do comportamento de grandezas variáveis cuja variação depende de outras grandezas, como a distância percorrida por um objeto em movimento em função do tempo; a temperatura em um ambiente em cada posição no espaço; o número de indivíduos em uma população com o passar do tempo etc.
Em cálculo, duas noções têm papel central no estudo de fenômenos assim: a taxa de variação local (ou instantânea) e a acumulação global – expressas na matemática, respectivamente, pelos conceitos de derivada e de integral.
Para entender a primeira, precisamos falar primeiramente da taxa de variação média, que corresponde à razão entre as variações de duas grandezas y e x, com a primeira dependente da segunda em um intervalo dado para a grandeza x. Representamos essa razão por Δy/Δx.
Exemplo concreto: no caso de um objeto em movimento, temos a distância percorrida s dependendo do tempo t. A taxa de variação média, então, é a divisão da distância percorrida Δs em um intervalo de tempo Δt, ou seja, Δs/Δt, que é a velocidade média nesse intervalo de tempo.
De forma mais geral, quando temos uma grandeza que depende de outra, a taxa de variação média expressa o quanto a primeira grandeza varia em relação à variação da segunda.
Se a dependência entre essas grandezas for representada graficamente (figura 3A), a taxa de variação média corresponde à inclinação da reta que passa pelos pontos correspondentes ao intervalo em questão – quanto mais inclinada for essa reta, mais acentuada será a variação de uma grandeza em relação à outra nesse intervalo.
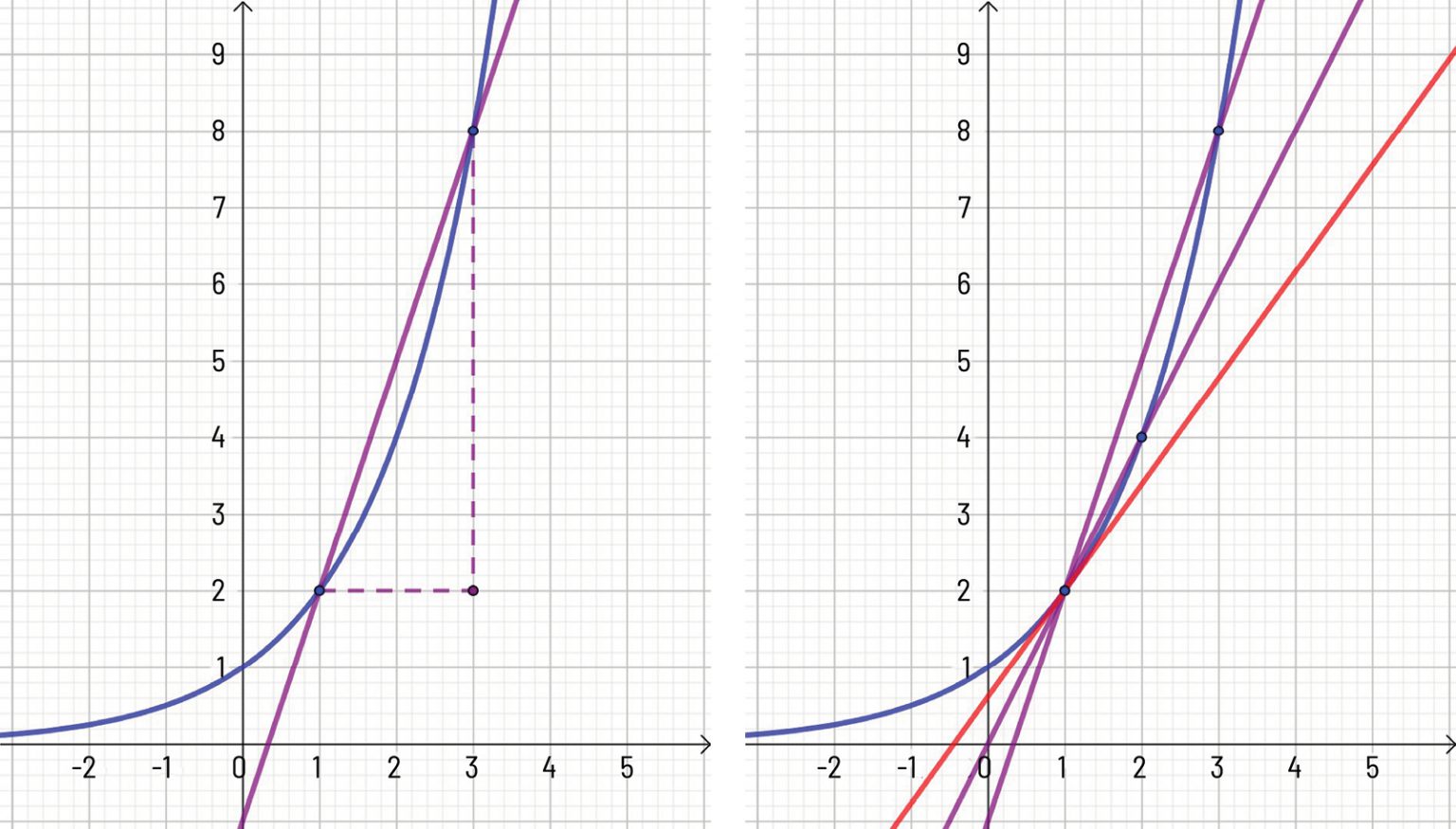
A taxa de variação local (ou derivada) corresponde ao valor do qual a taxa de variação média se aproxima, ao tomarmos intervalos de variação arbitrariamente pequenos, isto é, o valor do qual Δy/Δx se aproxima, quando Δx tende a zero (figura 3B).
Assim, a taxa de variação local (ou instantânea) corresponde à ‘passagem ao limite’ da taxa de variação média, ou, em certo sentido, à variação de uma grandeza em relação à outra – não em um intervalo, mas em um único instante.
A questão é que, se tentarmos calcular uma taxa de variação instantânea diretamente por meio de uma conta de divisão aritmética, esbarraremos em uma divisão de zero por zero – o que não tem sentido algebricamente, pois não existe número que seja resultado dessa conta.
Mas a taxa de variação instantânea ganha sentido por meio do conceito de limite – pois, mesmo com Δy e Δx tendendo ambos a zero, é possível que a divisão entre eles se aproxime de um número.
O conceito de derivada possibilita estudar em detalhes fenômenos envolvendo variação de grandezas, determinando, com precisão, quão acentuada é a variação de uma grandeza (distância percorrida, temperatura, população etc.) em cada instante.
Quanto mais acentuada for a variação, mais inclinado será o gráfico que representa uma grandeza que depende de outra. Assim, podemos determinar quando uma grandeza cresce ou decresce, bem como quando atinge um valor máximo ou mínimo.
Por meio do que chamamos de equação diferencial, é possível, também, determinar a posição de um objeto em movimento ao longo do tempo, caso conheçamos sua posição inicial e sua velocidade ao longo do movimento.
No caso da determinação de órbitas em Estrelas além do tempo, a aplicação do conceito de derivada possibilita saber, com precisão, que alterações pontuais na trajetória e velocidade de cápsula espacial devem ser feitas para resultar na trajetória desejada, para trazer seu tripulante de volta à Terra em segurança.
Já a integral tem a ver, como dissemos, com a noção de acumulação global. Caso relativamente simples: a determinação da área de um retângulo.
Uma forma de entender a área dessa figura como produto do comprimento dos lados é pensar em um deles ‘deslizando’ ao longo do outro (figura 4A). Desse modo, a área do retângulo torna-se resultado da acumulação do comprimento de um de seus lados ao longo do outro. Assim, a acumulação global de infinitos valores da grandeza ‘comprimento’ resulta em outra natureza: a área.
Sabendo determinar a área de um retângulo, podemos determinar a área de qualquer triângulo (dividindo por dois). E, com base na área de um triângulo, somos capazes de achar a área de qualquer figura delimitada por segmentos de reta, por meio de sua decomposição em triângulos.
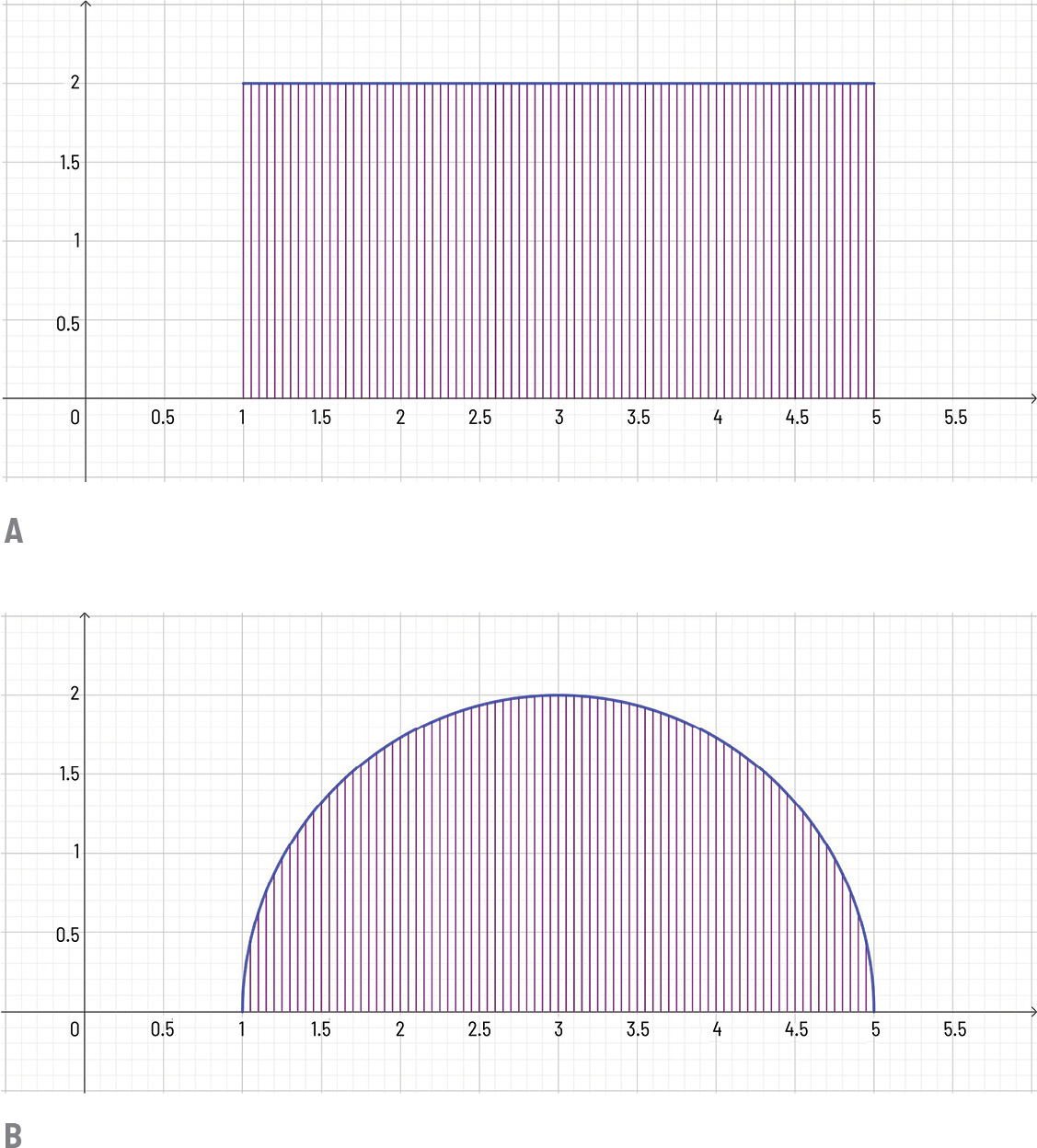
Mas como determinar a área de figuras delimitadas por curvas e não por segmentos de reta? Por exemplo, um círculo? A área de uma figura desse tipo também pode ser entendida como uma acumulação infinita de comprimentos.
Mas, nesse caso, diferentemente do retângulo, esses comprimentos não têm necessariamente um valor constante (figura 4B). Nessa formulação, a área é entendida como acumulação global (ou integral) de comprimentos variáveis.
Modo equivalente de determinar áreas de figuras delimitadas por curvas é por meio de aproximações infinitas por figuras formadas por segmentos de reta, como retângulos ou triângulos. Por exemplo, a área de um círculo pode ser determinada por meio de aproximações infinitas por polígonos regulares inscritos ou circunscritos a ele. Nesse método, os valores das áreas dos polígonos ficam arbitrariamente próximos quando aumentamos indefinidamente o número de seus lados (figura 5).

As alegadas dificuldades em cálculo certamente estão relacionadas com a profundidade teórica de seus conceitos fundamentais – especialmente, com o fato de esses envolverem noções de infinitos e de infinitésimos.
Mas essa afirmação é vaga e insuficiente para entendermos por que o cálculo é considerado tão difícil. Essas dificuldades não podem ser entendidas só a partir dos conceitos que integram seus currículos, de maneira abstrata, sem levar em consideração as formas como esses currículos têm sido concebidos e praticados.
Na década de 1950 e na seguinte, quando se situa Estrelas além do tempo, começou a se estabelecer um modelo de disciplina de cálculo para cursos universitários da área de exatas, desenhado com um objetivo político específico: formar, em grande escala, profissionais (especialmente, engenheiros) com perfil técnico, capazes de empregar as ferramentas do cálculo para resolver manualmente problemas aplicados não triviais, de forma rápida e precisa.
Naquela época, esse objetivo era imposto pela disputa por poderio tecnológico na Guerra Fria. A ausência das tecnologias digitais disponíveis hoje impunha, ainda, a necessidade de usar os conceitos do cálculo como ferramentas para resolver à mão problemas aplicados – o que não exige necessariamente compreensão teórica desses conceitos.
Assim, à época, o modelo de cálculo que se estabeleceu era mais focado na execução de procedimentos e no domínio de ferramentas do que na compreensão mais teórica de seus conceitos fundamentais subjacentes.
Esse modelo se consolidou e se disseminou na forma de currículos e livros, influenciando até hoje o ensino do cálculo (inclusive, no Brasil), apesar das grandes transformações sociais e tecnológicas das últimas seis décadas.
Internacionalmente, tem-se debatido a atualização dos currículos das carreiras em ciências, tecnologia, engenharias e matemática, identificadas pela sigla, em inglês, STEM (science, technology, engineering and mathematics).
Essas discussões têm enfatizado a importância de consolidar uma formação mais criativa, crítica e humana nessas áreas, levando em conta tanto a disponibilidade de recursos tecnológicos digitais quanto a necessidade de enfrentamento das questões sociais e científicas contemporâneas.
No Brasil – ainda que essas discussões tenham se dado mais timidamente –, é importante refletirmos sobre as dificuldades, a sensação de desconexão com a realidade relatada por estudantes, bem como os altos níveis de reprovação associados a essa disciplina, à qual, não raramente, atribui-se uma imagem mítica.
A que proposito essa imagem serve? É importante refletirmos sobre até que ponto essas dificuldades estão mais relacionadas à profundidade teórica inerente aos conceitos fundamentais do cálculo do que às formas como eles têm sido abordados nos currículos.
O caráter tecnicista herdado de outros tempos tem dado ao ensino do cálculo abordagem anacrônica na formação de cientistas, professores de educação básica ou profissionais técnicos – uma abordagem desconectada das transformações sociais e tecnológicas nas últimas décadas.
O enfretamento de problemas contemporâneos – alimentados politicamente pelo negacionismo científico – demanda formação de profissionais em exatas com mais sensibilidade para o reconhecimento dos compromissos sociais da ciência.
Isso, no entanto, não implica em ‘superficialidade’ ou ‘facilitação’ do ensino do cálculo, nem desmerecimento da profundidade de seus conceitos fundamentais – essa disciplina segue essencial para o enfrentamento de problemas contemporâneos de caráter técnico-científico com apelo social, ambiental e econômico.
No Brasil, a universidade precisa olhar seriamente para o ensino de graduação, pela perspectiva política voltada a seu papel social. Isso envolve não só políticas de permanência de estudantes nos cursos de graduação, mas também posicionamentos sobre o perfil dos egressos.
Devemos nos perguntar a que propósito servem disciplinas em início de graduação que atuam como ‘filtros’ para a permanência de estudantes? Quem são os estudantes que permanecem e quem são aqueles ‘filtrados’?
Afinal, queremos formar profissionais críticos e socialmente comprometidos em ciências exatas ou continuar a produzir ‘computadores humanos’?
Para finalizar, deixo às leitoras e aos leitores frase do líder indígena, intelectual e escritor Aílton Krenak, de seu livro Ideias para adiar o fim do mundo (2019): “Há muito tempo não existe alguém que pense com a liberdade do que aprendemos a chamar de cientista”.
Victor Giraldo
Programa de Pós-graduação em Ensino de Matemática,
Programa de Pós-graduação em Educação,
Universidade Federal do Rio de Janeiro