Novas tecnologias desenvolvidas na UFRJ ampliam o acesso de estudantes com deficiência visual à disciplina, inclusive no ensino superior.

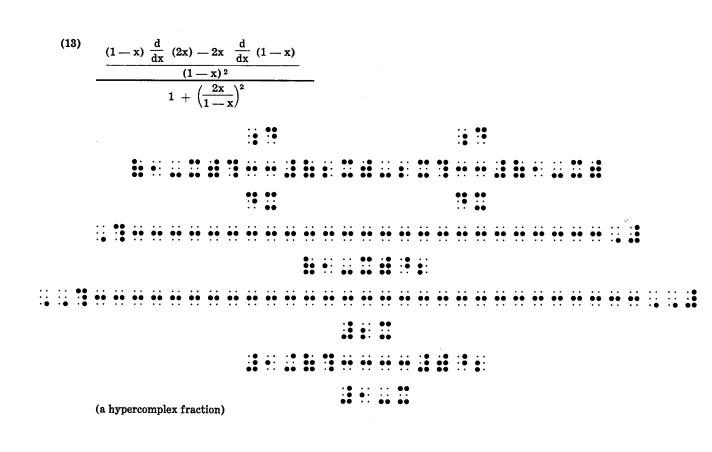
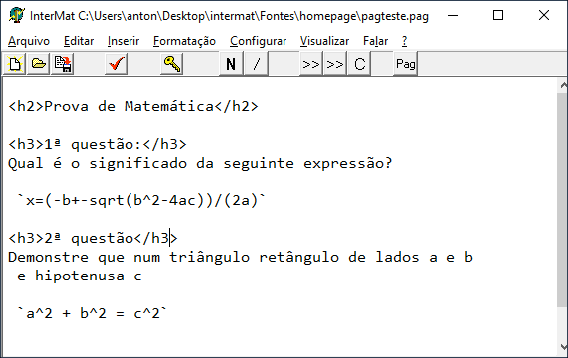
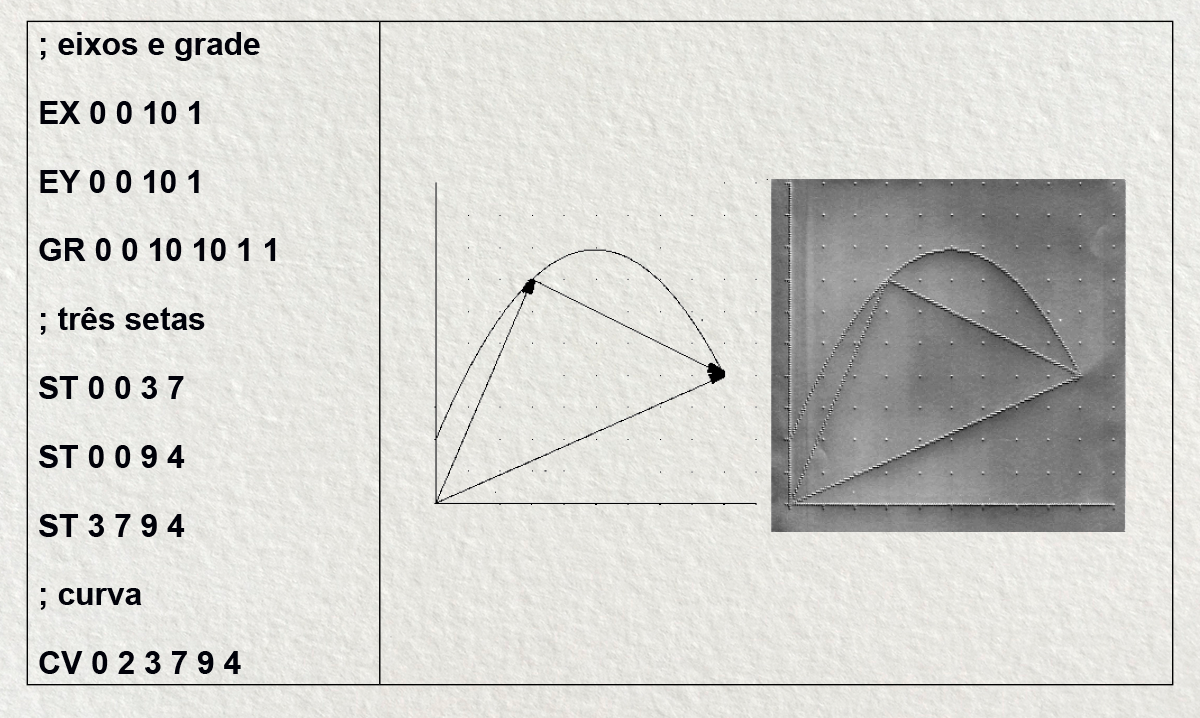
O número de estudantes cegos nas escolas públicas vem aumentando nos últimos anos como resultado das recentes leis de inclusão do Brasil. Mas grande parte desses estudantes está excluída do processo de ensino-aprendizagem em muitas disciplinas, em particular na matemática. Os principais entraves são a leitura, a manipulação e a escrita de símbolos matemáticos. Felizmente, hoje já é possível minimizar essas dificuldades, com ajuda da tecnologia de computação e aplicação de técnicas pedagógicas.

Um pouco de história

Hoje são muitas as pessoas com deficiência visual formadas em diferentes áreas, graças à tecnologia. Qual seria a razão, então, de tão poucos cegos estarem em cursos ligados à matemática? O raciocínio da disciplina seria incompatível com as restrições impostas pela cegueira? Afinal, a matemática é baseada em um processo interativo de leitura e manipulação de símbolos, onde a visão é parte essencial, e o significado de uma expressão matemática não é facilmente traduzido em palavras.

Há exemplos que desmentem essa afirmação. Talvez o mais impressionante seja o do matemático inglês Nicholas Saunderson (1682-1739), que viveu em uma época em que não havia tecnologia de escrita para cegos. Mesmo assim, ele é considerado um dos maiores matemáticos da história – ocupou na Universidade de Cambridge (Reino Unido) a posição de Professor Lucasiano, assim como o físico e matemático inglês Isaac Newton (1643-1727) e o físico teórico e cosmólogo britânico Stephen Hawking (1942-2018). Mas Saunderson era um superdotado, formulava e resolvia equações complexas de cabeça. Uma pessoa cega, com capacidade intelectual comum, precisa de técnicas especiais de escrita e leitura para desenvolver sua habilidade matemática.

Nicholas Saunderson, cego e um dos maiores matemáticos da história.

A matemática em Braille

Foi só em 1824 que Louis Braille, um estudante cego, desenvolveu um sistema eficaz de escrita e leitura autônoma para pessoas com deficiência visual. O método Braille, que usa símbolos em relevo resultantes da combinação de pontos dispostos em duas colunas e três linhas, permite que o cego escreva e leia textos e, com pequenas adaptações, transcreva símbolos musicais e expressões matemáticas simples.

Expressão matemática em Braille.

Entretanto, à medida que a complexidade aumenta e os elementos matemáticos não ficam todos em uma mesma linha (como frações, potências, raízes), é necessário introduzir componentes inexistentes na fórmula original transcrita. Somente assim, é possível manter os símbolos Braille lado a lado – algo essencial para leitura fluente com os dedos. A expressão, por exemplo, será transcrita em Braille em algo como (x+y)/(z+1), usando pontinhos, naturalmente.

Durante mais de cem anos, essa foi a única alternativa. E apenas nas escolas especializadas, dedicadas exclusivamente ao ensino fundamental, com professores habilitados para utilizar escrita matemática Braille. Mas isso não acontecia nas instituições de ensino regulares.

Novas perspectivas

Com a popularização do computador, tecnologias foram desenvolvidas nos Estados Unidos, mas não puderam ser adotadas no Brasil. Por aqui, em 1993, o softwareDosvox– desenvolvido pelo Núcleo de Computação Eletrônica (NCE) da Universidade Federal do Rio de Janeiro (UFRJ)– ampliou o uso do computador para cegos, para leitura e escrita, mas pouco oferecia quando o assunto era matemática.

Em 2017, a Lei Brasileira de Inclusão levou milhares de cegos às universidades. A minoria que ingressou em cursos de exatas e tecnológicas enfrentou imensas dificuldades. Era urgente desenvolver soluções. Simplificando, havia dois problemas para o aluno cego:

1. Escrever matemática no computador, com ferramentas simples, usando uma escrita linear (algo semelhante ao que os programadores fazem quando criam programas convencionais em um editor de textos de linhas de comando).

2. Ler um texto matemático escrito por ele próprio ou por outras pessoas, traduzindo o texto criado para uma fala que o representasse de forma clara.

As alternativas mais óbvias eram os formatos LaTeX, usado por 90% dos matemáticos para gerar textos científicos, ou o MathML, usado pelos navegadores da web para mostrar textos matemáticos. Infelizmente, ambos são complicados de escrever e sua leitura usando síntese de voz, quase ininteligível. Uma terceira alternativa foi escolhida: o formato AsciiMath, uma forma fácil de escrever matemática para a qual a renderização (geração do gráfico em papel) era compatível com todos os navegadores da atualidade.

Fórmula transcrita pelo formato AsciiMath: é fácil, usando um sistema de transcrição, gerar a forma matemática à direita em um navegador web ou no papel..

Ainda que um cego, devidamente orientado, possa escrever matemática com grande precisão e beleza com o AsciiMath, ele não conseguiria ler a fórmula com facilidade.  Para isso, foi desenvolvido no NCE/UFRJ o Sonora Mat, uma ferramenta de leitura e elaboração de textos matemáticos.

Essa solução foi integrada ao Sistema Dosvox, que, a partir de 2018, passou a editar e imprimir fórmulas matemáticas de grande complexidade, misturadas a textos comuns, bastando para isso que os textos em AsciiMath fossem precedidos e sucedidos por um caractere especial. Essa metodologia foi consolidada em um programa de livre distribuição, o Intermat, para pessoas com e sem deficiência.

Exemplo do que pode ser feito no programa Intermat, que pode ser usado por pessoas com e sem deficiência.

Gráficos: a última fronteira

Em matemática, o desenho é crucial para complementar a informação escrita. Quanto mais técnico é o que desejamos escrever, mais o desenho se firma como uma linguagem gráfica na qual podemos expressar ideias e dados de maneira concisa, clara e interessante.

Até pouco tempo atrás, as tecnologias de desenho para cegos disponíveis permitiam apenas a leitura ou a escrita, em alguns casos indireta, ou com interveniência de outros dispositivos. A verdade é que os cegos não têm sido levados a desenhar, apenas a consumir os gráficos. Felizmente, algumas soluções surgiram para mudar essa realidade.

A figura mostra um pequeno gráfico gerado no Grafivox, impresso automaticamente em tinta e em impressora Braille.

Foi desenvolvida também no NCE/UFRJ uma pequena linguagem gráfica chamada Grafivox, compatível com o sistema Intermat, que contempla a criação de entidades geométricas com rapidez e versatilidade. Os comandos dessa linguagem são expressos por abreviaturas de duas letras (por exemplo, RT para reta, RG para retângulo), seguidas por coordenadas cartesianas, polares, relativas, fórmulas ou pontos descritos a partir de arquivos. Um interpretador produz em uma tela (impressora comum ou Braille) o desenho automaticamente escalonado.

Foi comprovado, a partir de experiências com alunos cegos na UFRJ, que o estudante pode produzir, com treinamento mínimo, gráficos legíveis para pessoas cegas ou não. Esse programa só se viabilizou pela disponibilidade das impressoras Braille e das máquinas fusoras, hoje presentes em centros de apoio pedagógico nas escolas públicas.

Próximos passos

Graças à tecnologia de computação e a dispositivos de reprodução específicos, abriram-se novas perspectivas para o ensino de matemática a cegos, inclusive no nível superior. As barreiras agora são o domínio dessas ferramentas pelos professores. Felizmente, mecanismos para disseminação dessas técnicas, principalmente via educação a distância, prometem capacitar os docentes para o ensino de matemática com o nível esperado para todos os brasileiros. Com ou sem deficiência.