Quando pedimos ajuda para chegarmos a um destino, frequentemente, recebemos instruções do tipo “Siga em frente; logo depois da padaria, vire à direita e continue; depois, vire na primeira à esquerda…”. A razão para termos instruções assim é simples: para navegarmos em qualquer lugar, precisamos saber, literalmente, como nos orientarmos. É fundamental sabermos os ângulos para virarmos em pontos cruciais (no caso, padaria, esquina…).

Esse modo de navegar vale tanto para um bairro quanto para a Terra. Para o globo terrestre – na ausência de pontos de referência simples, como padarias e esquinas –, criamos um sistema de coordenadas que nos permite localizar um ponto na superfície do planeta. Esse sistema é formado por arcos de círculo que vão de um polo a outro – os meridianos, que nos dão a longitude de um ponto – e por círculos que cortam a Terra paralelamente ao plano da linha do equador – daí, o nome de paralelos, que nos dão a latitude.

Imagine um meridiano como sendo um grande arco de círculo que pode girar, como uma porta de banco, pelo eixo que passa pelos polos. Tomando como ponto de referência o meridiano que passa pelo Observatório Real de Greenwich (Inglaterra), o meridiano primário, medimos o ângulo que temos que girar para passarmos por um ponto qualquer do globo. Esse ângulo é medido de 0^o a 180^o no sentido oeste-leste e de 0^o a 180^o negativos no sentido oposto. Esse ângulo é a longitude do ponto.

Como todos os pontos em um mesmo meridiano têm a mesma longitude, precisamos de mais informação – obtida a partir da latitude. De modo semelhante, a latitude é medida pelo ângulo que temos que ‘subir’ ou ‘descer’ em relação ao plano equatorial. Esse ângulo é positivo e vai de 0^o a 90^o no sentido que leva ao polo Norte e negativo (de 0^o a – 90^o) em sentido ao polo Sul.

Com essas duas informações, podemos encontrar qualquer ponto do planeta. Mas como os navegadores usam essa informação?

Historicamente, essa informação tinha que ser impressa em uma folha de papel – mais modernamente, pode ser mostrada em uma tela de vídeo –, para facilitar sua visualização e seu transporte. O problema que surge aqui é que a superfície da Terra é, em boa aproximação, uma esfera, mas uma folha de papel ou tela são planas.

Como podemos passar a informação de uma superfície para a outra, preservando os ângulos entre curvas que se cruzam?

Seguindo o exemplo das instruções para o deslocamento em um bairro, gostaríamos de ter um mapa que nos orientasse, preservando ângulos entre curvas, do mesmo modo que usamos o “vire à direita” ou “vire à esquerda”. Para isso, é importante entender o que é um ângulo entre duas curvas, pois, normalmente, pensamos em ângulos entre segmentos de linha reta.

Para entender um ângulo entre curvas em uma superfície qualquer, podemos usar a ideia de que, ‘vista de muito perto’, uma superfície curva pode ser aproximada por um plano. Quando analisamos um campo de futebol, não nos preocupamos com a curvatura da Terra, por exemplo.

Dizemos que estamos analisando as curvas localmente. Desse ponto de vista, a definição de ângulo é a que usamos normalmente (ou seja, entre segmentos de linha reta), e isso nos permite definir o ângulo entre duas curvas quaisquer. Transformações geométricas que preservam os ângulos entre curvas são tão importantes que merecem nome especial: transformações conformes.

O modo de pô-las em prática é razoavelmente simples: apoie uma esfera em um plano e ‘sente-se’ no polo norte dela – ‘N’, na figura 1, onde ‘O’ é o centro da esfera, e ‘S’, o polo sul. Para um ponto qualquer na superfície da esfera (P), trace uma reta que une esse ponto ao polo norte.

Essa reta irá intersectar o plano em algum ponto. Esse ponto (P’) é a projeção estereográfica do ponto P na superfície da esfera – podemos repetir esse procedimento para todos os pontos da esfera, obtendo para cada um deles sua projeção estereográfica. Em tempo: provar matematicamente que essa projeção preserva ângulos entre curvas requer um pouco mais de trabalho, e, para nossos propósitos aqui, vamos dispensá-lo, para evitar tecnicalidades.

A projeção estereográfica preserva os ângulos entre duas curvas que se cruzam – como as da latitude e longitude –, mas não preserva áreas. Áreas próximas ao polo norte (tanto terrestre quando de uma esfera) ficam ampliadas. É por isso que, apesar de a Groenlândia ter área de aproximadamente 2.166.000 km², ela parece, nos mapas planos, maior que o Brasil, com aproximadamente 8.516.000 Km².

Claro que a escolha do ponto onde ‘nos sentamos’ para fazer a projeção estereográfica é arbitrária e, dependendo dela, o resultado é uma orientação e dimensão particular ao mapa-múndi. Com base na escolha desse ponto – no caso, o polo Sul terrestre –, o artista uruguaio Joaquín Torres-García (1874- 1949) fez provocação interessante com sua obra América invertida (figura 2).

Não bastasse a grande utilidade de uma transformação conforme em nos permitir produzir um mapa extremamente útil para a navegação, ela tem outras aplicações. Por exemplo, na descrição de fenômenos relacionados aos estados da água, a um ímã  ou a partículas subatômicas, como veremos.

Uma experiência simples do dia a dia é o que acontece com a água, à medida que ela é aquecida. Começando com gelo, ele vai se derreter até se liquefazer completamente e, em seguida, evaporar. Essas mudanças são conhecidas como transições de fase.

Podemos repetir esse mesmo experimento a diferentes pressões. Se ajustarmos a pressão e temperatura de maneira cuidadosa, podemos chegar a um ponto ‘mágico’ da água, no qual não há mais diferença entre vapor e líquido (figura 3). Esse é o chamado ponto crítico. Vale notar que esse ponto não acontece no dia a dia, mas em situação controlada de laboratório. Nele, coisas interessantes acontecem.

Para entendermos o que se passa no ponto crítico, dois conceitos são importantes: simetria e comprimento de correlação.

A simetria de um sistema é uma ação (transformação) que fazemos nele que o deixa idêntico à configuração inicial. Por exemplo, se girarmos um quadrado em 90^o por um eixo perpendicular que passa por seu centro, a nova figura será idêntica à inicial. Dizemos que o quadrado é invariante por rotações de 90^o.

A natureza é invariante com base em várias simetrias, como a de rotação ou translação. Por exemplo, se analisarmos a estrutura cristalina do gelo – ou seja, o  modo como os átomos de hidrogênio e oxigênio estão dispostos –, veremos que é possível girá-la em 60^o, e o resultado permanecerá idêntico. Nesse caso, dizemos que o gelo tem simetria hexagonal – aliás, uma bela consequência dessa simetria é sua relação com flocos de neve (figura 4).

As simetrias têm consequências profundas para os fenômenos naturais: elas não só implicam leis de conservação, ou seja, quantidades que não mudam com o tempo (por exemplo, a conservação da energia), mas também dão estrutura às leis da natureza.

Entender quais são as simetrias de um sistema físico permite deduzir, de forma bem específica, como devem ser as possíveis soluções de dado problema. Exemplo: o fato de existir uma simetria de translação espacial no universo – ou seja, o fato de podermos nos transladar de um ponto a outro do espaço, sem que as leis da natureza se alterem – é o que nos permite realizar experimentos em diferentes laboratórios. E a simetria de translação temporal é o que nos permite fazer experimentos em momentos diferentes (passado, presente e futuro).

Mas há simetrias que surgem dinamicamente. Elas ‘aparecem’ ao mudarmos certos parâmetros do sistema que estamos investigando. Vejamos o caso do gelo derretendo e virando água. O número de mudanças (rotações) que podemos realizar na estrutura cristalina do gelo – deixando-a invariante – é pequeno.

Mas, ao derreter completamente, devemos levar em conta a simetria da água em estado líquido, cuja estrutura tem agora uma nova simetria, diferente daquela do cristal de gelo: em vez de podermos girar apenas em 60^o ao redor de certos eixos, qualquer rotação é permitida.

Vejamos agora o segundo daqueles dois conceitos citados como importantes: o comprimento de correlação, que dá ideia de qual a distância entre partes de um sistema que apresentam comportamentos semelhantes.

Exemplo: imagine ladrilhos encaixados de forma precisa, cobrindo o chão. Se soubermos a posição de um deles, saberemos a posição de todos os outros – tecnicamente, dizemos que a posição dos ladrilhos é fortemente correlacionada, e o comprimento de correlação é grande.

Mas, caso os ladrilhos não estejam bem encaixados, a análise de um deles pode nos dar a ideia incerta sobre a posição do seguinte. E, à medida que nos afastamos do ladrilho inicial, podemos perder completamente a informação de onde o próximo ladrilho deverá estar. Nesse caso, dizemos que o comprimento de correlação é finito.

No caso extremo – ladrilhos simplesmente jogados um ao lado do outro –, a posição de um deles não nos diz nada sobre a dos outros. O comprimento de correlação é zero.

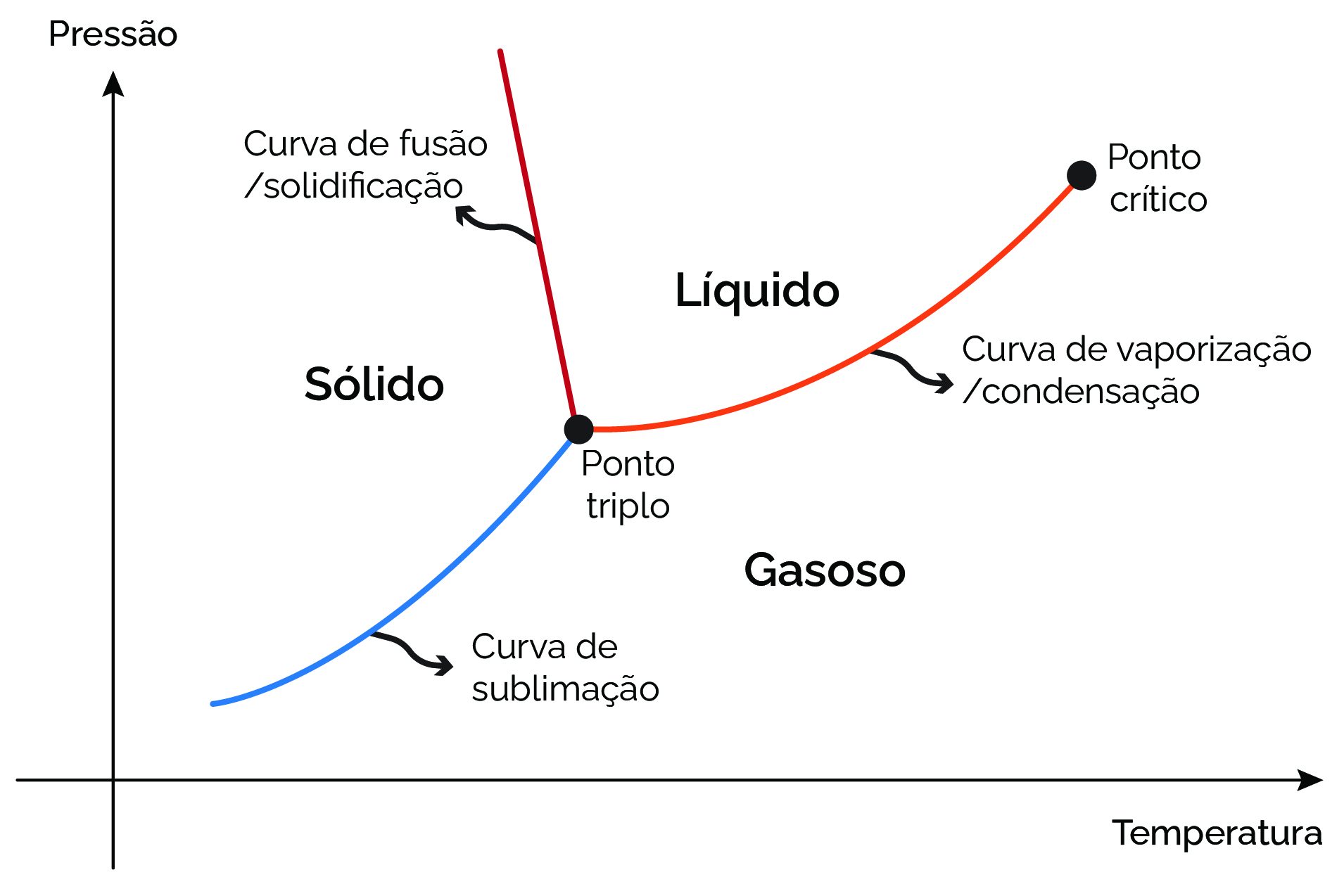
Agora, podemos voltar à questão que lançamos acima: o que simetrias e comprimento de correlação têm a ver com o ponto crítico da água? Nesse ponto, o comprimento de correlação se torna grande – tecnicamente, dizemos que ele diverge –, e o sistema não tem mais uma escala de comprimento, ou seja, mesmo pontos muito distantes entre si estão correlacionados. Surge uma nova fase da água.

A consequência disso é que o sistema líquido-vapor pode ser descrito matematicamente por uma teoria que é invariante por transformações conformes. E, aqui, entra o tão importante conceito de simetria: surgem novas simetrias no sistema, a chamada invariância conforme, que nos permite estudar com precisão quantitativa o ponto crítico.

Até aqui analisamos o que se passa com a água. Mas o surpreendente (e belo) é que a mesma linguagem usada para descrever o ponto crítico da água pode ser empregada para descrever o que se passa em outros sistemas físicos bem diferentes, como um ímã.

Apesar de toda familiaridade que temos com ímãs – basta olhar para uma geladeira… desde os ímãs que prendem a porta até aqueles que seguram lembretes e desenhos –, a explicação de como ‘funcionam’ não é tão simples.

Essencialmente, um ímã é formado por ‘mini-ímãs’, que têm sua origem em propriedades dos elétrons e dos átomos em si. Sabemos que um ímã tem um polo norte e um sul, mas isso só ocorre caso os mini-ímãs estejam orientados em uma direção. Se estiverem distribuídos aleatoriamente – imagine-os como diminutas bússolas cujas agulhas apontam em várias direções –, seus efeitos se cancelam. Resultado: o ímã macroscópico não vai atrair agulhas, pregos etc. Ou seja, não será um ímã.

Seria possível restaurar a magnetização, a propriedade que faz um ímã atrair outros metais?

A resposta é sim. Basta reduzirmos sua temperatura, o que fará com que cada mini-ímã ‘sinta’ os companheiros em sua vizinhança e comece a se alinhar com eles – nesse caso, teríamos todas as agulhas das diminutas bússolas apontando em uma única direção.

Para os ímãs, há também um ‘ponto crítico’ – no caso, temperatura crítica. Abaixo dela, o sistema se magnetiza. É nesse ponto (ou temperatura) que o comprimento de correlação se torna grande (diverge), pois mesmo mini-ímãs distantes apontam para a mesma direção. Com isso, surge uma nova simetria no sistema: sim, a invariância conforme.

Apesar de os dois sistemas (transição líquido-gás na água e magnetização de um ímã) serem tão distintos, a descrição teórica dos dois é semelhante. E não só de forma qualitativa: eles têm várias propriedades matemáticas em comum, as quais variam segundo as mesmas leis. Dizemos que pertencem à mesma classe de universalidade.

Na década de 1970, foi proposta uma ideia revolucionária segundo a qual as partículas elementares não seriam entidades pontuais, mas, sim, pequenas cordas dotadas de diferentes modos de vibração. Cada um deles corresponderia a uma partícula que observamos na natureza, como elétron, próton, fóton (partícula de luz) etc.

Essa nova formulação se mostrou promissora não só por explicar a origem das diferentes partículas elementares, mas também por elucidar a existência de uma partícula que daria origem à gravidade, o gráviton.

No caso da teoria de cordas, a invariância conforme também tem papel fundamental. Se uma partícula, ao se deslocar no tempo e espaço, descreve uma linha, uma corda em movimento descreve uma superfície. A partir dessas linhas e superfícies é possível calcular uma quantidade matemática chamada ação, fundamental para deduzir as equações que governam o movimento de partículas ou cordas. Em particular, existem transformações matemáticas que não alteram o valor da ação. Estas são justamente as transformações conformes.

Desde o nascimento da teoria de cordas, houve avanços em seu entendimento, mas ela segue como um trabalho em andamento. Mesmo assim, esse é um caminho promissor, que pode nos levar a uma teoria que junte, em um só corpo teórico, tanto os fenômenos microscópicos, da física quântica, quanto aqueles das grandes escalas (estrelas, galáxias, buracos negros etc.), da gravidade. Ou seja, uma teoria quântica da gravidade.

Mapas de nosso planeta, transições de fase da água, ímãs, gravitação quântica… Uma gama impressionante de aplicações distintas unidas por uma linguagem matemática comum, a das transformações conformes.

A sensação que temos ao perceber isso é perfeitamente traduzida pelo poeta britânico William Blake (1757-1827): “Ver um mundo em um grão de areia/E um paraíso numa flor selvagem/Segure o infinito na palma da sua mão/E a eternidade em uma hora”.