Um joguinho popular – cujo desafio é encontrar rapidamente figuras em comum entre duas cartas – está baseado em conceitos ‘ocultos’ de uma área da matemática: a geometria projetiva finita, que lida basicamente com pontos e linhas que se cruzam

Um joguinho popular – cujo desafio é encontrar rapidamente figuras em comum entre duas cartas – está baseado em conceitos ‘ocultos’ de uma área da matemática: a geometria projetiva finita, que lida basicamente com pontos e linhas que se cruzam

A geometria é o ramo da matemática que trata das propriedades do espaço (distâncias, formas e áreas). Até o século 19, falar em geometria era falar em geometria euclidiana – referência a Euclides (3 a.C.), que sistematizou o conhecimento da área até aquele momento.
Esse matemático grego fez isso com base em axiomas – proposições consideradas autoevidentes – e regras de dedução lógica. Exemplos: “por dois pontos, passa uma única reta” (axioma) e “se A é igual a B, e B igual a C; então, A é igual a C” (dedução lógica).
A partir do fim do século 19, surgiram outras geometrias. Por exemplo, a projetiva, como desdobramento da técnica da perspectiva usada por artistas.
A geometria projetiva trata de pontos e linhas – qual ponto está em qual linha; quais linhas se cruzam –, como na perspectiva, e não de distâncias e ângulos. Ambas têm conceitos semelhantes, como os ‘pontos no infinito’ (geometria projetiva) e ‘pontos de fuga’ (arte) – estes últimos podem ser observados, por exemplo, nas margens de uma longa estrada reta.
Os ‘pontos de fuga’ lembram um conceito da geometria euclidiana, o das retas paralelas, as quais nunca se cruzam. Na geometria projetiva, porém, não existem retas paralelas, pois todas se cruzam.
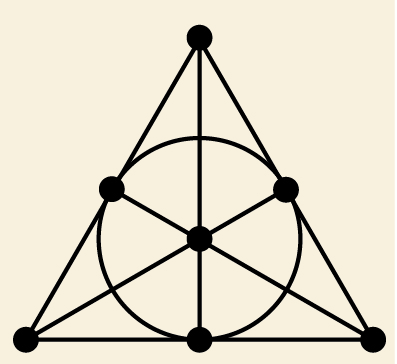
A geometria projetiva tem uma subárea: a geometria projetiva finita, que lida com um número finito de pontos e linhas. Exemplo dela está na figura a seguir: o ‘plano de Fano’, homenagem ao matemático italiano Gino Fano (1871-1952). Nela, temos sete pontos e sete linhas – no caso, os lados e as alturas do triângulo, bem como o círculo.
Para acessar este ou outros conteúdos exclusivos por favor faça Login ou Assine a Ciência Hoje.

Um dos principais nomes da IA generativa, o cientista da computação Hao Li vislumbra um futuro em que a tecnologia será capaz de criar humanos digitais, reconstituir o passado e construir metrópoles em tempo real. Mas ele reconhece dilemas éticos: ‘O importante é as pessoas saberem o que é possível’

Cientistas de diversas áreas do conhecimento e diferentes nacionalidades desenvolveram um algoritmo capaz de identificar as barragens que poderiam gerar eletricidade de forma mais vantajosa, causando o menor dano possível na região
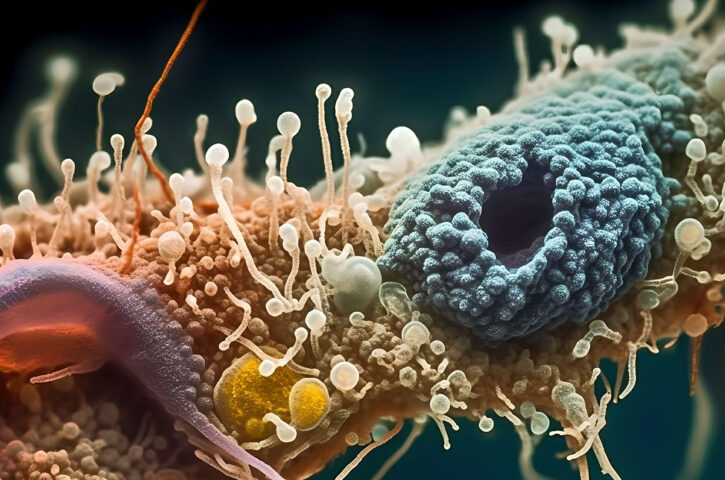
“Aquilo que sabemos é pouco; o que não sabemos é imenso”. A frase atribuída ao cientista francês Pierre-Simon Laplace (1749-1827) cai sob medida para o quanto ainda desconhecemos sobre a diversidade dos protozoários, diminutos seres onipresentes na natureza

Por que insetos caminham sobre a água? Por que se forma o orvalho? A explicação para esses fenômenos começou ainda na Antiguidade. Hoje, a ciência das interações intermoleculares tem aplicações na medicina e na indústria – e no cotidiano

A macroecologia é uma área multidisciplinar que estuda padrões de biodiversidade em grande escala. Essa disciplina inovadora tem também ajudado nos estudos sobre mudanças climáticas, como ferramenta para a elaboração de políticas de sustentabilidade.

Entender a natureza dos fatores envolvidos na origem desse transtorno mental pode ajudar na busca por novas formas de tratamento. Evidências mostram que intervenções sobre o sistema imune podem beneficiar alguns pacientes com essa condição psiquiátrica

O uso de mecanismos genômicos no tratamento das doenças de Alzheimer ou Parkinson pode produzir perspectivas terapêuticas importantes. Estudos recentes mostram que uma versão de um determinado gene pode conferir proteção contra essas enfermidades.
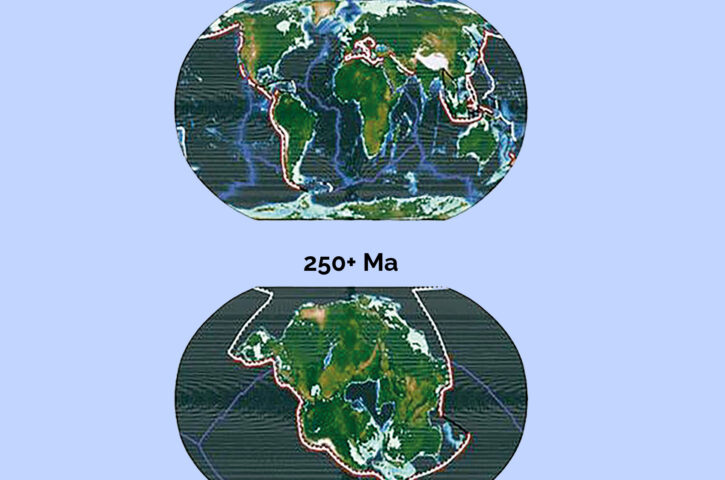
Pesquisadores projetam que a formação de uma extensa massa continental, denominada Pangeia Última, daqui a cerca de 250 milhões de anos, vai gerar condições climáticas extremas, sobretudo um aquecimento global que irá restringir as regiões habitáveis do planeta

Os prêmios Nobel de Física e Química deste ano contemplaram trabalhos que investigaram a matéria em sua mais diminuta escala: a atômica e subatômica. E esses resultados têm aplicações práticas que vão da área eletrônica até o tratamento do câncer

Duas irmãs e duas amigas delas. Todas as quatro excelentes tenistas. Elas decidem disputar, entre elas, um torneio do tipo ‘perdeu, tá fora’. Qual a probabilidade de as duas irmãs se enfrentarem? Soa complicado. Mas a matemática está aí para simplificar as coisas

Uma intoxicação atinge amigos em um acampamento. No hospital, o médico de plantão enfrenta problema sério: como dar a cada paciente o maior número possível de doses de uma vacina (sem exceder o limite seguro), quando os três tipos de imunizante vieram sem rótulos?

Claro, Noel e seu ‘simpático’ ajudante, Gunther, apareceram. Desta vez, abriram presentes, comeram bolo e usaram – para variar – um truque ‘desleal’: apresentaram ao dono da casa um problema fácil para, depois, complicar as coisas. Mas, no fim, foi divertido

Seguimos com o joguinho popular cujo desafio é encontrar rapidamente figuras em comum entre duas cartas. Neste mês, exploraremos questões intrigantes e ainda desafiadoras para a matemática: dado certo número de figuras, quantas cartas terá nosso jogo?

Uma reflexão (mental) sobre os espelhos nos revelará que esses objetos escondem ‘mistérios’ não só interessantes, mas também úteis – tanto aqui na Terra quanto no espaço. Depois de ler esta coluna, você terá outra imagem sobre essas superfícies refletoras.
Um jogo simples em que cada participante deve escolher um número dentro de certo intervalo tem uma resposta lógica (e surpreendente) se os jogadores forem matemáticos. Mas, no mundo real, a coisa é mais bem complicada, como mostram os economistas

Quatro copos sobre uma mesa giratória. Problema: deixá-los todos virados para cima ou para baixo. Trivial? Sim. Mas, agora, faça isso com os olhos vendados, e esse desafio se torna um jogo muito interessante do ponto de vista lógico. Difícil? Não se preocupe: a matemática, mais uma vez, vai te ajudar.

Máximus, o mágico, está de volta. E vem com um truque que, como sempre, deixará Vítor, seu assistente-vítima, surpreso e espantado. Desta vez, o mestre das ilusões nos apresenta uma tabela com propriedades intrigantes. Seja bem-vindo, bem-vinda, a mais um show de ‘matemágica’!

Teoria da probabilidade causa ‘derrapadas’ até mesmo em matemáticos experientes, pois a aleatoriedade pode dar um ‘nó’ em nossos cérebros. Mesmo problemas aparentemente simples podem levar a resultados distintos: é preciso saber não só ‘o que’ se calcula, mas ‘como’ se faz isso

O velhinho de barbas longas e seu insuportável ajudantezinho deram as caras de novo. E, desta vez, com uma oferta irrecusável: pedaços de barra de chocolate. Será que Noel é um ser redimido e, este ano, vai finalmente ser generoso comigo, sem truques, surpresas (desagradáveis), enganação? Ou...?

Um tutor se diverte com seu vira-lata em um parque, ambos dando voltas em torno de uma árvore. Nessa cena corriqueira do cotidiano, está embutido um teorema de consequências profundas e importantes para a matemática. Mais: ele pode ser entendido só com palavras, sem qualquer cálculo.
| Cookie | Duração | Descrição |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |
